Menu
1
 Icône RSS Icône RGPD     Nombre de visiteurs : 2 188 371     actuellement :
(record :		 2 connectés
39) 		    Dernière mise à jour le 08/02/2024 Version mobile

II - NOMBRES COMPLEXES, ARITHMÉTIQUE, POLYNÔMES ET ÉQUATIONS

 

Table des matières :

  1. Nombres complexes
  2. Opérations d'arithmétique
  3. Calculs sur les polynômes
  4. Equations
  5. Exercices

 

 

1. Nombres complexes

Comme vu au chapitre 1, Maple est capable de faire des calculs symboliques sur les nombres complexes grâce à sa variable I (notre i complexe) qui est donc une des deux solutions complexes de l'équation x2 = –1 (d'ailleurs on l'obtient par la commande solve(x^2=-1, x); qui renvoie alors I, –I). Par convention, on pose i2 = –1.

  > (2+5*I)+(1-I)+5*(3+6*I);
  (4+6*I)*(7-9*I);
  (6+2*I)/(1-I);
  (2+8*I)^2;
 

18 + 34I
82 + 6I
2 + 4I
–60 + 32I

 

Remarques :
• Les règles de calcul pour développer (a + bi)2 sont les mêmes, cette quantité vaut a2 + 2abi – b2 ;
• On a vu que Maple préfère donner le résultat de la manière la plus formelle possible. Pour les complexes, Maple s'efforcera toujours de donner le résultat sous la forme algébrique a + bi ;
• Maple possède aussi des commandes spécifiques aux nombres complexes, comme le montre l'exemple suivant :

  > z:=2+3*I;       # on définit un complexe z, et on peut alors avoir...
  Re(z);          # ... sa partie réelle
  Im(z);          # ... sa partie imaginaire
  abs(z);         # ... son module
  argument(z);    # ... son argument
  conjugate(z);   # ... son conjugué
 

 

Représentation usuelle et représentation exponentielle : Comme chacun le sait, tout nombre complexe z peut s'écrire de manière ordinaire, sous la forme z = a + bi, ou de manière exponentielle, sous la forme z = ρ e iθ, où ρ est le module de z et θ son argument. En Maple, un nombre complexe de module 2 et d'argument π/4 se note polar(2, Pi/4);.

• Passer de la forme traditionnelle à l'exponentielle : on utilise la commande convert (consultez l'aide en ligne, car cette commande peut convertir bien plus que des nombres complexes...). Par exemple, un nombre complexe 3 – 4i s'écrira de la manière suivante sous forme exponentielle : convert(3-4*I, polar); ;

• Passer de la forme exponentielle à la traditionnelle : on utilise dans ce cas evalc ("évaluation de complexes"). En effet, la ligne evalc(polar(sqrt(2), Pi/4)); renverra un nombre complexe sous la forme a + ib, comme le montre l'exemple suivant.

  > polar(sqrt(2), Pi/4);          # nombre complexe de module 2 et d'argument Pi/4
 

  > evalc(polar(sqrt(2), Pi/4));   # renvoie ce nombre sous sa forme traditionnelle
  convert(1+I, polar);
 

1 + I

 

2. Opérations d'arithmétique

Calcul avec les modulo : Maple peut aussi effectuer des calculs modulaires. Il y a la simple commande mod, traditionnellement utilisée en Mathématiques. Mais on a aussi les commandes modp et mods, qui différent quelque peu. En effet, le calcul (par exemple) modp(14, 5); donne le même résultat que 14 mod 5; (c'est-à-dire 1). Par contre, le calcul mods(14, 5); donnera le résultat –1. En effet, mods évalue le reste de la division euclidienne de a = 14 par b = 5. Si ce dernier est supérieur à la moitié du diviseur |b| (ce qui est le cas ici, puisqu'il vaut r = 4), alors il renvoie r – |b| = –1. "mods" et "modp" donnent respectivement des représentations symétrique et positive d'un calcul modulaire.

  > 16 mod (-6);
  modp(16,-6);
  mods(16,-6);
 

4
4
-2

 

PGCD, PPCM, nombres premiers et factorisation d'entiers : Maple étant un logiciel anglophone, on ne peut (malheureusement !) par calculer les PGCD et PPCM à partir des mêmes noms. En fait, en anglais, PGCD se dit « Integer Greater Common Divisor » et PPCM se traduit par « Integer Less Common Multiple ». Ainsi, on appelle ces deux formules par les commandes igcd ou ilcm, que l'on peut appliquer à un ou plusieurs nombres.

  > igcd(24, 4);
  igcd(6160, 8372, 56);
 

4
28
  > ilcm(38, 341);
  ilcm(6, 9, 18);
 

12958
18

Un nombre est dit premier s'il n'est divisible que par 1 et lui-même. Étant donné que 1 n'admet que lui-même pour diviseur, il ne fait pas partie des nombres premiers. Il est conseillé de connaître la liste des nombres premiers jusqu'à 100 : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. Maple intègre plusieurs fonctions qui traitent des nombres premiers. Soit a un entier supérieur ou égal à 1. On a alors les fonctions suivantes :
• isprime(a)   :  revoie true si a est premier et false sinon ;
• ithprime(a)  :  renvoie le aième nombre premier ;
• nextprime(a) :  renvoie le plus petit nombre premier supérieur ou égal à a.

  > isprime(77); isprime(79);
  ithprime(1); ithprime(10);
  nextprime(50); nextprime(100);
 

false
true
1
29
53
101

De plus, le théorème fondamental d'algèbre nous assure que tout nombre entier supérieur ou égal à 1 peut se décomposer de manière unique en produit de nombres premiers. En Maple, cette opération s'effectue simplement par la commande ifactor (le "i" pour "integer" !!).

 

3. Calculs sur les polynômes

Introduction : C'est maintenant que les choses un peu plus sérieuses commencent, puisqu'on commence à mettre les pieds dans le calcul utilisant des expressions symboliques. Commençons ici par les plus simples d'entre elles : les polynômes. Puisque ce sont en particulier des fonctions, nous allons les définir de la même manière, et nous constatons alors déjà les premières propriétés des polynômes (évaluation en un point, addition, quotient, factorisation, développement, ...) :

  > P1 := x -> 3*x^2+4*x+1;
  P2 := x -> x^3-1;
  P1(y); P2(x);
 

P1 := x → 3x2 + 4x + 1
P2 := x → x3 - 1
3y2 + 4y + 1
x3 - 1

  > P1(0); P1(-1); P2(0); P2(1);
  Q := x -> P1(x)+P2(x);
  R := x -> P1(x)/P2(x);
  Q(0); R(0);
 

1
0
-1
0
Q := x → P1(x) + P2(x)

0
-1

  > factor(P1(x)); factor(P1(2));
  S := x -> (P1(x))^2: S(x);   # rappel : le ":" ne fait pas afficher le résultat
  expand(S(x));
 

(x + 1) (3x + 1)
(x – 1) (x2 + x + 1)
(3x2 + 4x + 1)2
9x4 + 24x3 + 22x2 + 8x + 1

 

Factorisation : Revenons un peu à la factorisation. En fait, dans Maple, la factorisation d'un polynôme se fait dans le plus petit corps contenant tous les coefficients du polynôme considéré. Pour ceux qui ne comprennent pas, retenez simplement que factor(x^2 - 2); renverra x2 – 2 (car x et 2 sont alors considérés comme des entiers relatifs), tandis que factor(x^2 - 2.); renverra (x + 1.414213562) (x – 1.414213562) (car x et 2. sont considérés comme des flottants). Cependant, pour que la première factorisation puisse être faite dans le corps des réels, on peut préciser à Maple que la factorisation se fait par rapport à un élément. Ainsi factor(x^2-2, sqrt(2)); renverra alors le "bon" résultat (x + ) (x – ).

On peut factoriser des polynômes de plusieurs variables avec cette commande. En effet,

  > factor(x^3-y^3);
 

(x – y)(x2 + xy + y2)

 

Autres fonctions utiles sur les polynômes :
1) On va commencer par citer collect, qui permet de regrouper les termes d'un polynôme selon une variable (ou une expression) donnée. On peut aussi factoriser les expressions qui ont été collectées. Par exemple,

  > P := x,y,z -> x^2-y^2+2*z^2+x*y-2*x*y^2+3*y*z;
  collect(P(x,y,z), x);
  collect(P(x,y,z), x, factor);
 

P := x → x2 – y2 + 2 z2 + xy – 2 xy2 + 3 yz
x2 + (– y2 + y) x + 2 z2 + 3 yz – y2
x2 – y (2y – 1) x + 2 z2 + 3 yz – y2

  > Q := x -> a^3*x–x+a^3+a;
  collect(Q(x), x);
  collect(Q(x), x, factor);
 

Q := x → a3 x – x + a3 + a
(a3 – 1) x + a3 + a
(a – 1) (a2 + a + 1) x + a (a2 + 1)

2) Deux commandes utiles peuvent être normal, qui met des fractions de polynômes au même dénominateur, et sort, qui trie un polynôme selon ses puissances décroissantes :

  > 1/(1+x)+x/(x^2-3)+x^2/(x-1);
  normal(%);
  sort(%);
 

3) On peut aussi utiliser la commande simplify, qui demande à Maple de simplifier au maximum le résultat qu'il a trouvé précédemment.

  > (x^5-3*x^3-x^4+2*x+4)/(x^4+x-2*x^3-2);
  simplify(%);
 

Il faut cependant faire attention !! Le résultat qui s'affiche après cette commande n'est pas toujours le résultat qu'on voit sous forme "habituelle", tel que nous l'aurions nous-mêmes simplifié. Il se trouve que Maple oublie parfois des simplifications élémentaires. En effet, lorsque l'on tape (-1)^(2*n), il est évidemment sous-entendu que cela vaut 1, mais pour Maple, n n'est pas forcément un entier, donc il retourne (–1) (2n). Nous verrons ultérieurement (solution de l'exercice 17, c du chapitre 4) comment remédier à ce problème (commande subs).

Nous avons déjà vu quelques fonctions élémentaires qui agissent sur tout un polynôme. Nous allons maintenant voir deux fonctions qui permettent d'extraire des éléments d'un polynôme.

 

Degré d'un polynôme : Il s'agit de degree, qui extrait le degré d'un polynôme d'une variable. Dans le cas de plusieurs variables, on peut préciser selon laquelle on voudrait extraire le degré, et par défaut, Maple extrait le degré total (c'est-à-dire qu'il considère toutes les variables comme étant par exemple x, et renvoie le degré de ce polynôme à une variable), comme le montre l'exemple suivant :

  > P := x -> -4*x^4+2*x^5+x^2-3*x;
  degree(P(x));
 

P := x → – 4 x4 + 2 x5 x2 – 3 x
5

  > Q := (x,y) -> 3*x^4*y+2*x^2*y^3-x+2*y-2;
  degree(Q(x,y), x); degree(Q(x,y), y);
  degree(Q(x,y));
 

Q := x → 3 x4 y + 2 x2 y3 – x + 2 y – 2
4
3
5

 

Coefficients d'un polynôme : La commande permettant d'extraire un coefficient d'un polynôme est coeff. On précise en attribut le monôme dont on veut le coefficient. Quant à la commande lcoeff, elle permet de donner le coefficient du monôme de plus haut degré dans le polynôme.

  > P := x -> -4*x^4+2*x^5+x^2-3*x;
  coeff(P(x), x^3); coeff(P(x), x^2);
  lcoeff(P(x));
 

P := x → – 4 x4 + 2 x5 + x2 – 3 x
0
1
2

 

4. Équations

Maple sait résoudre (quelle chance !!) toutes sortes d'équations : équations linéaires, systèmes, équations différentielles, équations numériques, etc. La commande principale pour résoudre une équation est solve. Maple est aussi capable de travailler sur des équations plus générales (par exemple, donner la formule qui donne les racines d'un polynôme du second degré), auquel cas, il faut bien préciser quelle est l'inconnue (ce qui n'est pas forcément le cas quand il n'y a qu'une variable, mais prenez l'habitude de le faire quand même).

  > eqn := 2*x^2-8;
  solve(eqn);       #fonctionne, mais préférez solve(eqn, x);
  solve(eqn, {x});
 

eqn := 2 x2 – 8
2, -2
{x = 2}, {x = -2}
  > eqn := a*x^2+b*x+c;
  solve(eqn, x);  # Correct !
  solve(eqn);     # Attention...
 

Remarques : Les deux lignes successives eqn := 2*x^2-8; solve(eqn, {x}); sont exactement équivalentes à l'unique ligne solve(2*x^2-8, {x});. En fait, on peut ne pas passer par l'affectation de l'équation dans une variable (qui est ici eqn), mais on peut directement effectuer le calcul. De plus, lorsque l'on précise entre accolades l'inconnue, Maple précise de quelle variable de l'équation il s'agit (dans le dernier exemple, avant-dernière ligne, on ne sait pas directement sans regarder la commande si Maple a résolu l'équation en x, a, b ou c !!).

 

Systèmes d'équations : Il s'agit de la même commande, mais les différentes équations sont mises entre accolades, ainsi que les différentes variables :

  > solve({x+2*y=3, x+y=1}, {x,y});
 

{y = 2, x = -1}

Parfois, il arrive que Maple donne les solutions d'un système sous la forme RootOf(...), ce qui signifie "racines de ..., ce qui n'est pas très explicite. Il convient alors de demander à la ligne suivante allvalues(%), qui donne alors toutes les valeurs possibles de cette solution bizzaroïde. Essayez de résoudre le système suivant : x + y = 1 et x – y2 = 2.

 

Solutions numériques : La commande fsolve (« floatting solve », soit résolution en flottants) sert à résoudre les équations et à exprimer leur(s) solution(s) de manière approchée. Il faut cependant se méfier, car pour un polynôme de degré 5, qui admet donc forcément 5 racines complexes (rien n'empêche que quelques unes soient réelles, car l'ensemble des réels est inclus dans l'ensemble des complexes), Maple ne donnera que les valeurs approchées des solutions réelles. Tout comme solve, on peut mettre l'inconnue souhaitée entre accolades :

  > P := x -> x^4-x^3+x^2-x-1;
  fsolve(P(x), x);
  fsolve(P(x), {x});
 

P := x → x4 – x3 + x2 – x – 1
-.5187900637, 1.290648801
{x = -.5187900637}, {x = 1.290648801}

fsolve dispose cependant de pas mal d'options intéressantes. On pourra consulter l'aide en ligne, mais les plus importantes sont l'ajout en option d'un intervalle de définition où l'on souhaiterait que la solution appartienne, ou le mot clé complex qui donnera alors les valeurs approchées complexes. Reprennons l'exemple précédent (en supposant que P soit encore en mémoire) :

  > fsolve(P(x), x, x=0..5);    # ou fsolve(P(x), {x}, x=0..5);
  fsolve(P(x), {x}, complex);  # ou fsolve(P(x), x, complex);
 

{x = 1.290648801}
{x = -.5187900637}, {x = .1140706312 + 1.216746004 I}, {x = .1140706312 – 1.216746004 I}, {x = 1.290648801}

Autres équations : Il existe aussi les commandes isolve (« integer solve »), permettant de donner les solutions entières d'une équation (très pratique pour la relation de Bézout ou les équations diophantiennes) et msolve (« modulo solve ») qui donne les solutions d'une équation modulo un certain entier m. Pour ce dernier, consulter l'aide en ligne si nécessaire (très peu utilisé en fait). Dans l'exemple qui suit, _Z1 désigne pour Maple n'importe quel entier relatif (d'où le Z !). Le Z ayant le même indice 1 dans x et y, c'est le même entier (sinon on aurait eu x = 2 + 3 _Z2).

  > isolve(5*x-3*y=4);
 

{y = 2 + 5 _Z1, x = 2 + 3 _Z1}

 

5. Exercices

  1. Exercice 4
    a. Donnez une représentation polaire de z1 = 6 + iπ ;
    b. Donnez les parties réelles et imaginaires de z2 = (3 – 6i)3i ;
    c. Soient z3 = i – 1 et z4 = 2i. Donnez les modules et arguments de z3 et z4 ;
    d. Mettez le quotient z3 / z4 d'abord sous forme algébrique, puis sous forme polaire ;
    e. Facultatif : Donnez les modules et argument de z2. Cela vous semble-t-il logique ? Essayer de trouver un moyen de contourner le "problème".

  2. Exercice 5
    a. Soient a = 1049427 et b = 17493. Quel est le PGCD de a et b ? Ce PGCD est-il premier ?
    b. Décomposez a et b en produits de nombres premiers. Quelle doit être la décomposition du PPCM en nombres premiers ?
    c. Calculer le résultat de 773 3570 (mod 3571) et de 123 3570 (mod 3571). Si n est un entier compris entre 1 et 3570, quel doit être le résultat de n 3570 (mod 3571) ?
    d. Quel est le 500ième nombre premier ? Quel est le nombre premier qui suit 40000 ?
    e. Facultatif : Donnez la décomposition en produits de facteurs premiers de 200! (factorielle de 200). D'après vous, de combien de zéro le nombre 200! se termine-t-il ?

  3. Exercice 6
    a. Factorisez les deux polynômes suivants : P1(x) = x4 – 1 et P2(x) = x3 + x2 – 5x – 5. Que vaut le polynôme P1(x) / P2(x) ?
    b. Définissez le polynôme suivant : poly(x, y, z) = (x2 – a) (xy + b) (x4 – y4) (3x + z) (z – x). Développez, simplifiez ce polynôme, puis ordonnez-le d'abord selon x, puis selon y et enfin selon z ;
    c. Quel est la valeur du coefficient de x5 dans le polynôme défini à la question 2 ? Même question pour y3.

  4. Exercice 7
    Déterminez toutes les solutions de l'équation ex – 3x = 0.

  5. Exercice 8
    a. Résoudre le système suivant :
        
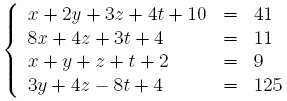
    b. Résoudre le système suivant :
        
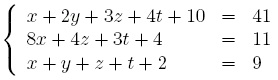
    c. Résoudre le système suivant :
        
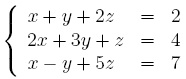
    c. Résoudre le système suivant :
        

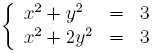
  6. Exercice 9
    a. Trouvez une solution réelle strictement positive de l'équation tan(x) – x = 0 ;
    b. Trouvez une solution approximative de l'équation tan(sin(x)) = 1 lorsque x varie entre –π et π.