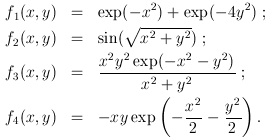III - GRAPHIQUES

Table des matières :

Graphiques en 2 dimensions
D'autres types de graphes en 2D
Graphiques en 3 dimensions
Animations
Exercices

Nous rentrons maintenant plus dans des spécificités de Maple, mais qu'il faille toujours savoir manier. Pour commencer, Maple dispose de plein d'outils qui permet la réalisation de graphiques en tous genres. La syntaxe générale pour tracer un graphique est plot_type(expression, intervalle, options), où :
• plot_type désigne le type de graphique qu'on veut réaliser (2D, 3D, paramétrique, ...) ;
• expression est une ou plusieurs expressions mathématiques qui définissent la (ou les) fonction(s) à tracer ;
• intervalle est de la forme x=a..b (avec a < b) (cela peut aussi être une liste d'éléments dans le cas de fonctions de 2 variables (graphes 3D)) ;
• options est un ensemble d'accessoires qui permettent d'ajuster le graphique (mettre un titre, couleur des tracés, échelles, ...).

La commande de base pour tracer des graphes 2D en Maple est plot. Il est vivement conseillé de consulter l'aide en ligne. Il existe cependant beaucoup d'autres commandes qui permettent de tracer des graphiques divers. Il existe même une librairie (i.e. un ensemble de fonctions prédéfinies), appelée plots, que l'on peut charger dans la mémoire de Maple au début d'une feuille Maple, via la commande with(plots):. Si l'on remplace : par ; dans cette instruction, Maple va afficher les noms des nouvelles fonctions à l'écran, en plus de les charger en mémoire.

1. Graphiques en 2 dimensions

Le type de graphique le plus simple que nous puissions reproduire en Maple est une instruction du genre plot(f(x), x). À ces quelques caractères obligatoires viennet s'ajouter des paramètres optionnels pour obtenir une instruction plus complète du type plot(f(x), x=a..b, y=c..d, option1, ...). Comme le montre l'exemple suivant, plus on met de paramètres, plus "précise" est le tracé de la fonction. La fonction qu'on trace est f, dépendante de la variable x que l'on fait varier de a à b.

	> plot(1/x, x); plot(1/x, x=-2..2); plot(1/x, x=-2..2, y=-3..3);

Dans la suite, nous verrons les options les plus couramment utilisées. Pour les autres, vous pouvez toujours consulter l'aide en ligne de la fonction plot via la commande ?plot[option].

Introduction aux graphiques : Dans l'exemple précédent, on a tracé la fonction inverse sur l'intervalle [–2, 2]. Or on sait que cette fonction est discontinue en 0. Mais Maple essaye toujours dans ce cas de joindre les points de discontinuité. Pour éviter cela, il faut rajouter l'option discont=true. On le voit encore mieux sur l'exemple qui suit. Si l'on rajoute en plus l'option scaling=constrained, Maple va prendre la même échelle sur les deux axes, ce qu'on a préféré ne pas faire ici...

	> plot(x-floor(x), x=0..5); #floor désigne la partie entière plot(x-floor(x), x=0..5, discont=true);

Par défaut, Maple calcule un minimum de 50 points par graphe, mais il peut être utile (pour la précision du tracé) dans certains cas de lui demander d'en calculer plus. Cela se fait via l'option numpoints=500, comme le montre le graphe suivant d'une fonction de très petite amplitude :

	> plot(x^3sin(exp(1/x)), x=(.2)..(.3)); plot(x^3sin(exp(1/x)), x=(.2)..(.3), numpoints=500);

De manière générale, plusieurs courbes peuvent être tracées en même temps. Il faut mettre chaque courbe entre crochets, ainsi que les options correspondantes : plot([courbe1, ..., courben], x=a..b, color=[c1, ..., cn], thickness=[t1, ..., tn], ...). Montrons un exemple un peu plus illustratif !

	> plot([1/x, exp(sqrt(x)), abs(x)], x=-3..3, y=-3..3, color=[red, blue, green], thickness=[2,1,3], linestyle=[1,2,3]);

La libraire "plots" : On ne rentrera pas en détails ici dans les fonctions que renferme cette librairie, mais il faut quand même savoir (ce sera utile pour ceux qui continueront en licence de Mathématiques à Strasbourg...) qu'il existe un autre moyen de superposer des graphes. Il s'agit de la commande display de cette libraire. Pour pouvoir l'utiliser, il faut au préalable soit charger la librairie plots en entier (par with(plots):), qui contient donc cette fonction, soit charger simplement la fonction qu'on veut utiliser (par with(plots, display):), soit encore en l'appelant directement par plots[display] à la place de display. Ensuite, il faut mettre dans une variable le tracé d'une courbe, c'est-à-dire faire par exemple P1 := plot(..., x=a..b):. En effet, le tracé d'une fonction via plot est interprété par Maple comme une longue liste de points qu'il doit afficher à l'écran et relier entre eux. Si vous mettez un ; dans la dernière expression écrite, vous verrez un truc incompréhensible du genre P1 := PLOT(CURVES([ ici vient la longue liste de points ], COLOUR(RGB, 1.0, 0., 0.), AXESLABELS("x", "y"), VIEW(-3. .. 3., -3. .. 3.)). Ensuite, il suffit alors de taper display(P1);, et le tour est joué. Mais regardons plutôt l'exemple suivant :

> with(plots): ou with(plots, display)
P1 := plot(1/x,x=-3..3,y=-3..3,discont=true):
P2 := plot(x, x=-3..3, color=blue):
display(P1, P2);

Ceci est identique à :

	> # On ne charge pas de librairie P1 := plot(1/x,x=-3..3,y=-3..3,discont=true): P2 := plot(x, x=-3..3, color=blue): plots[display](P1, P2);

Remarque : Par rapport aux premières figures de cette page, où l'on avait déjà représenté la fonction inverse, on constate que le trait rouge présent sur l'axe des ordonnées a disparu, grâce à l'option discont=true. Par rapport à précédemment, cette méthode n'apporte pas encore grand chose de neuf. On va voir maintenant pourquoi elle peut être plus efficace.

Texte sur un graphe : Maple peut placer du texte un peu n'importe où sur un graphe de fonction. C'est la commande textplot (également du package "plots") qui se charge de ceci, et on procède comme précédemment, c'est-à-dire que le résultat de cette fonction va être placé dans une variable (par exemple T), qui sera utilisé par display :

	> with(plots): > P1 := plot(sin(x), x=-Pi..Pi): T1 := textplot([Pi/2, 1.2, `Maximum local`], font=[TIMES, ITALIC, 12]): T2 := textplot([-Pi/2, -1.2, `Minimum local`], font=[TIMES, ITALIC, 12]): display({P1, T1, T2}, title="f(x) = sin(x)", titlefont=[HELVETICA, BOLD, 18]);

Remarque : Ici, on utilise display sur plusieurs variables (P1, T1, T2), et des options. Il faut alors encadrer les variables par des accolades. En tant que remarque, on peut aussi citer que si une fonction (par exemple f) a été définie pour une seule variable, on peut la tracer simplement par l'instruction suivante : plot(f, a..b);, au lieu de plot(f(x), x=a..b);. Si on définit par exemple une suite de fonctions par f := (n,x) -> 1/(n*x);, l'instruction plot(f, a..b); ne donnera pas de résultat car Maple ne sait pas quelle est la variable qui varie entre a et b.

2. D'autres types de graphes en 2D

Courbes paramétrées : La syntaxe d'une courbe définie paramétriquement par le vecteur (f (t), g(t)), fonction du temps t est la suivante : plot([f(t), g(t), t=a..b], options);. Le fait qu'il y ait des crochets encadrant tous les paramètres est la seule différence par rapport au type de graphe étudié ci-dessus. Ainsi, de manière paramétrique, le cercle unité est donc obtenu par l'instruction plot([sin(t), cos(t), t=0..2*Pi], scaling=constrained);. Voici maintenant un autre exemple, plus "artistique" :

	> plot([(sin(t)-cos(t))^3-sin(t)+cos(t), # f(t) cos(t)^2-sin(t)^2, t=-Pi..Pi], # g(t) -2..2, -1..1, scaling=constrained, color=blue); # les options

On peut évidemment tracer plusieurs courbes paramétrées sur un même graphe, voire même des courbes normales et paramétrées sur un même graphe. Il y a évidemment la méthode utilisant display, qui demande donc que chaque courbe soit placée dans une variable, mais il y a aussi plot. On procède ainsi comme suit :

> # Plusieurs courbes paramétrées :
plot([[t^2, t, t=-1..1],                       # 1ère courbe paramétrée
        [2*sin(t), cos(t), t=0..2*Pi]],         # 2ème courbe paramétrée
       scaling=constrained, color=[red, blue]);
> # Une fonction normale et une paramétrée :
plot([(x-x^3)/4,                               # Une courbe normale
        [(sin(t)-cos(t))^3-sin(t)+cos(t),       # Une courbe...
          cos(t)^2-sin(t)^2, t=-Pi..Pi]],       # ...paramétrée
       x=-2..2, color=[red,blue]);

Champs de vecteurs en 2D : Surtout utile en physique, Maple sait tracer des champs de vecteurs (par exemple d'une force électrique, magnétique, ou encore gravitationnelle) définis sous la forme (f (x, y), g(x, y)). La commande pour tracer un tel champs de vecteur se trouve dans la librairie "plots", il s'agit de fieldplot,qui s'utilise de la manière suivante : fieldplot([f(x,y), g(x,y)], x=a..b, y=c..d, options). Par exemple (on suppose dorénavant qu'un package qui contient la fonction illustrée a été chargé en mémoire) :

	> fieldplot([y, -x], x=-10..10, y=-10..10, arrows=SLIM);

L'option arrows (= flèche en anglais) peut être égale à LINE, THIN, SLIM, THICK. L'option par défaut est THIN.

Fonctions implicites : En Mathématiques, ce sont les fonctions définies par la relation f (x, y) = c, où c est une constante. À nouveau, une fonction du package "plots" nous permet de tracer facilement ce genre de fonction, il s'agit de implicitplot, qui s'utilise exactement comme plot, sauf que la simple expression f (x, y) de plot est remplacée par l'équation implicite f (x, y) = c dans implicitplot. On peut utiliser cette commande pour tracer par exemple des coniques :

	> implicitplot(x^2/25+y^2/9=1, x=-6..6, y=-6..6, scaling=constrained);

Graphes de points : La simple commande plot permet aussi de créer des polygones quelconques. On utilise alors la syntaxe suivante : plot([[a1,b1], ..., [an,bn]]);. Si de plus, on a [a₁, b₁] = [a_n, b_n], alors on a une courbe fermée. Par ailleurs, si l'on ne veut pas que Maple relie les points, il suffit de rajouter l'option style=point.

	> plot([[-5,-3], [4,-1], [5,3], [-4,1], [-5,-3]]); # Courbe fermée plot([[-5,-3], [4,-1], [5,3], [-4,1], [-5,-3]], style=point);

D'autres systèmes de coordonnées : Il existe d'autre types de systèmes de coordonnées : polaires, hyperboliques, elliptiques. On n'étudiera ici que les coordonnées polaires. Cela s'effectue par l'option coords=polar. Mais cela n'est pas aussi simple qu'il n'y paraît. En effet, il faut d'abord bien comprendre ce que sont les coordonnées polaires.

Si M est un point du plan, on sait que les projections sur les deux axes du repère donnent les deux coordonnées cartésiennes du point. Une fonction dépendante d'une variable x est représentée dans un repère par la relation y = f (x). M étant un point du plan, on peut aussi le repérer par l'angle orienté que fait l'axe des abscisses avant le vecteur OM, angle que l'on note généralement ρ, et par la mesure ("norme" en langage mathématique) du vecteur OM, que l'on note r. Ainsi, une fonction dépendant d'un paramètre q peut être représentée dans un repère dit polaire par la relation r = f (ρ).

Considérons alors un point M du plan, qui a donc des coordonnées (x, y) dans le repère cartésien et des coordonnées (r, ρ) dans un repère polaire. On constate alors facilement que passer de l'un à l'autre est possible par les égalités suivantes :
x = r cos(ρ) ; y = r sin(ρ) ; r = (x² + y²) ^1/2 ; cos(ρ) = x/r ; sin(ρ) = y/r.

Le cercle unité déjà rencontré précédemment est donc la représentation polaire de la fonction f (ρ) = 1, pour tout angle ρ compris entre 0 et 2π : plot(2, t=0..2*Pi, coords=polar, scaling=constrained);. Voici donc un autre exemple :

	> f := theta -> 6/sqrt(4cos(theta)^2+9sin(theta)^2); plot(f(t), t=0..2*Pi, coords=polar, scaling=constrained);

Inégalités : On peut représenter les inégalités avec Maple par la commande inequal. Elle est assez rarement utilisée quand même, donc vous pourrez consulter l'aide en ligne pour plus de précision. On prendra soin de noter que c'est une fonction de la librairie "plots". De plus, il faut savoir qu'une ligne pleine contient des solutions et qu'une ligne pointillée ne contient pas de solutions.

	> inequal({y+2*x<4, y-x<-1, y>=0}, x=-3..3, y=-6..4, optionsexcluded=(color=yellow));

Échelles logarithmiques : Les commandes logplot, semilogplot et loglogplot permettent respectivement d'obtenir une échelle logarithmique sur l'axe des ordonnées, celui des abscisses ou les deux. Cela peut être pratique pour certaines fonctions :

	> logplot(10^x, x=0..10); semilogplot(2^(sin(x^(1/3))), x=1..100); loglogplot(x^17, x=0..10);

3. Graphiques en 3 dimensions

Comme pour les graphes dans le plan, Maple sait aussi bien tracer des graphes dans l'espace. La commande que l'on utilise est alors plot3d, dont l'utilisation est rigoureusement identique à celle de plot (à la différence près qu'il y a deux variables à spécifier). Ainsi une fonction f des variables x et y va se représenter par plot3d(f(x,y), x=a..b, y=c..d, options);. Par défaut, pour des graphes en 3D, Maple n'affiche pas d'axes, mais ce fait peut être corrigé par l'option axes=frame ou axes=normal ou encore axes=boxed. Regardons déjà ces quelques exemples :

	> # Un graphe en 3D : plot3d((x^2-y^2)/(x^2+y^2), x=-2..2, y=-2..2); > # Le même avec des axes : plot3d((x^2-y^2)/(x^2+y^2), x=-2..2, y=-2..2, axes=frame); > # Deux graphes en 3D : plot3d({x+y^2,-x-y^2}, x=-2..2, y=-2..2, axes=boxed); > # Une courbe paramétrée : plot3d([ssin(s), scos(t), ssin(t)], s=0..2Pi, t=0..Pi, axes=normal);

Tout comme la commande plot, plot3d utilise par défaut les coordonnées cartésiennes. L'utilisation de l'option coords permet alors à nouveau de passer d'un système de coordonnées à un autre. En trois dimensions, les systèmes le plus utilisés sont les coordonnées cylindriques et sphériques. Consultez l'aide en ligne pour plus de précisions. On peut aussi éventuellement avoir recours au package "plots", qui renferme directement les fonctions sphereplot et cylinderplot, mais à nouveau, on ne pourra qu'inviter à consulter l'aide en ligne, car des graphiques en trois dimensions seront rarement réalisés, encore moins en coordonnées autres que cartésiennes...

Dans l'exemple précédent, nous avons aussi pu apercevoir la syntaxe d'une fonction paramétrée par un vecteur (f (s, t), g(s, t), h(s, t)) est la suivante : plot3d([f(s,t), g(s,t), h(s,t)], s=a..b, t=c..d, options);. Par rapport à plot, ce n'est pas toute l'expression qui est entre crochets, il faut donc différencier le graphe d'une fonction paramétrée (dont les fonctions coordonnées sont entre [ ]) et le graphe de plusieurs fonctions (qui sont toutes entre { }). Voici quelques exemples :

> # Une première courbe en coordonnées sphériques :
plot3d((1.3)^x*sin(y), x=-1..2*Pi, y=0..Pi, coords=spherical, style=PATCH);
> # Une deuxième courbe en coordonnées cartésiennes :
plot3d(sin(x*y), x=-Pi..Pi, y=-Pi..Pi, style=HIDDEN);
> # Une courbe paramétrée :
plot3d([x*sin(y)*cos(y), x*cos(y)^2, x*sin(y)], x=0..2*Pi, y=0..Pi);
> # Plusieurs graphes en même temps :
plot3d({sin(x*y), x+2*y}, x=-Pi..Pi, y=-Pi..Pi, axes=frame);
> # Plusieurs courbes paramétrées :
c1 := [cos(x)-2*cos(0.4*y), sin(x)-2*sin(0.4*y), y]: # On se donne
c2 := [cos(x)+2*cos(0.4*y), sin(x)+2*sin(0.4*y), y]: # 4 vecteurs de
c3 := [cos(x)+2*cos(0.4*y), sin(x)-2*sin(0.4*y), y]: # courbes
c4 := [cos(x)-2*cos(0.4*y), sin(x)+2*sin(0.4*y), y]: # paramétrées
plot3d({c1,c2,c3,c4}, x=0..2*Pi, y=0..10, grid=[25,15], style=PATCH);
> # Un graphe en coordonnées sphériques (avec package plots) :
sphereplot(1, theta=0..2*Pi, phi=0..Pi, scaling=constrained, title="Sphère unité");
> # Deux graphes en coordonnées cylindriques (package plots) :
cylinderplot(theta, theta=0..4*Pi, z=-1..1);
cylinderplot(z, theta=0..2*Pi, z=0..1);
> # Et une courbe paramétré en coordonnées cyclindriques :
cylinderplot([s*t, s, cos(t^2)], s=0..Pi, t=-2..2);

4. Animations

Desfois, on a besoin de voir comment un graphe évolue par rapport au temps (qui sera donc une variable t). Ceci est possible en Maple par la commande animate, qui a la syntaxe suivante : animate(f(x,t), x=a..b, t=c..d);. Le paramètre qui varie donc dans cette instruction est le temps t. On peut faire varier à peu près n'importe quoi : les courbes en 2D, les courbes paramétrées, et même les courbes en 3D. On veillera juste à ce que la libraire "plots" soit chargée, car elle contient la commande animate.

> with(plots, animate, animate3d):
animate(sin(x*t), x=-10..10, t=1..2);
animate([a*cos(u), sin(u), u=0..2*Pi], a=0..2);
animate3d(cos(t*x)*sin(t*y), x=-Pi..Pi, y=-Pi..Pi, t=1..2);

On ne peut pas représenter ici le résultat obtenu. Pour voir l'effet que cela implique, tapez les lignes du haut dans Maple, validez. Vous verrez alors à l'écran 3 graphiques qui se suivent : un représentant sin(t), l'autre qui semble vide (il y a juste les axes), et un graphe 3D. Cliquez une fois sur l'un des graphes. Sous la barre des menus est apparue une autre barre d'outils, avec des icônes représentant un peu les même fonctions qu'un lecteur vidéo. Cliquez sur l'icône en forme de triangle (pointe vers la droite, "play the animation" est inscrit lorsque l'on passe la souris sur le bon bouton !!) et observez le résultat !!

5. Exercices

Exercice 10
a. Sur l'intervalle [0, ∞[, tracez les fonctions définies par f (x) = | x | ^1/2 et g(x) = x² dans un même graphique ;
b. Tracer la fonction h(x) = 1 – E(x), où E désigne la fonction "partie entière". On fera attention aux points de discontinuité ;
c. Tracer la fonction e(x) = x exp(– x), pour tout x > –1. Pensez-vous que la dérivée de cette fonction s'annule en un point de l'intervalle considéré ?
Exercice 11
a. Tracer sur un même graphe les fonctions définies par f₁(x) = 1 – x, f₂(x) = 1 – x²,f₅(x) = 1 – x⁵ et f₁₀(x) = 1 – x¹⁰, pour x ∈ [0, 1] ;
b. Tracer l'animation de la fonction f_n(x) = 1 – xⁿ, pour x ∈ [0, 1] et n variant de 1 à 10.
Exercice 12
Sur un même graphe, tracer en bleu les fonctions qui à x ∈ [–2π, 2π] associent respectivement x, –x et sin(ax), où a est un paramètre qui varie entre 0 et 100. Passez l'option numpoints à 200 et nommez votre graphe « Un signal sinusoïdal », avec une police Helvetica de taille 14 points.
Exercice 13
a. Tracez la courbe de la fonction f (ρ) = sin(3ρ), en coordonnées polaires, pour ρ ∈ [0, 2π] ;
b. Tracez la spirale définie par la fonction g(ρ) = ρ, pour ρ ∈ [0, 4π] ;
c. Tracez la courbe polaire paramétrée, donnée par le vecteur (r, ρ) = (sin(t), cos(t)), pour t ∈ [0, 2π], dans un repère othonormé ;
d. Tracez la courbe polaire définie par l'équation ρ = exp(r), pour r entre –3 et 3 (on prendra 1000 pour valeur de numpoints) (attention, il faut aussi préciser un intervalle pour ρ !!).
Exercice 14
a. Tracez la courbe définie par l'équation y² = 2x + 4, dans la fenêtre –2 < x < 1,5 et –3 < y < 3 ;
b. Tracez la fonction f définie sur l'intervalle [0, 4] par :

width="304" height="105" alt=""/>
Exercice 15
Quelle est la région du plan satisfaisant ces inégalités : x ≤ 4, x > 0 et x + y ≤ 5 ?
Exercice 16
Toutes les fonctions suivantes sont à tracer, et sont définies sur le rectangle [–5, 5] x [–5, 5] :