|
1
|
|
Nombre de visiteurs : | 2 192 143 | actuellement : (record : |
2 connectés 39) |
Dernière mise à jour le 08/02/2024 | Version mobile |
|
1
|
|
Nombre de visiteurs : | 2 192 143 | actuellement : (record : |
2 connectés 39) |
Dernière mise à jour le 08/02/2024 | Version mobile |
Comme nous l'avons vu dans l'introduction, \(\LaTeX\) est en réalité un ensemble de commandes permettant de signifier au logiciel ce que l'on
a l'intention d'écrire : une formule mathématique, une citation, un théorème, etc. Même le contenu de ces diverses possibilité peut être
constitué de commandes. Je rappelle qu'une commande, en \(\LaTeX\), est toute instruction débutant par un antislash
(\).
Certaines de ces instructions ne nécessitent aucun argument (comme \alpha, ou
\Rightarrow, voir paragraphe 1), d'autres nécessitent un argument obligatoire (comme
\sqrt{5}, voir paragraphe 2) ou plusieurs (comme \frac{1}{2x}) et les dernières qui
nécessitent un argument obligatoire mais aussi éventuellement un argument facultatif (comme \sqrt[n]{5}, voir
paragraphe 2).
Il faut savoir que tout ce qui est mathématique doit être écrit dans un environnement dédié : pour simplifier, il existe l'environnement en ligne
(par exemple L'identité remarquable $(a+b)(a-b)=a^2-b^2$ qui donne "L'identité remarquable \((a+b)(a-b)=a^2-b^2\)") et
l'environnement qui centre l'écriture mathématique sur la ligne suivante (la même chose avec \[ et \] au lieu de
$ donnerait "L'identité remarquable \[(a+b)(a-b)=a^2-b^2\]").
Si un argument obligatoire ne se compose que d'un caractère ou n'est constitué que d'une seule commande, on peut ne pas le (la) mettre entre accolades :
\sqrt{5} et \sqrt5 renvoient le même résultat,
de même que \frac{1}{2} et \frac12,
ou encore \frac{3}{7x} et \frac3{7x} (on ne peut pas enlever les accolades du second argument, il serait sinon constitué de deux caractères !),
ou enfin \sum_{i=1}^{\infty} et \sum_{i=1}^\infty afficheront le même résultat (le second argument n'est pas constitué d'un seul caractère, mais c'est une commande).
Par contre, \lim_{n\to\infty} et \lim_n\to\infty ne donnent pas le même résultat : \(\lim_{n\to\infty}\) et \(\lim_n\to\infty\). En effet, dans le second cas, l'accolade n'est ni constituée d'un seul caractère, ni d'une seule commande, ce qui fait que \(\LaTeX\) ne considère comme argument obligatoire que le caractère n.
Vous avez noté que \(\LaTeX\) n'écrit pas la limite comme on le voudrait car il s'efforce dans un environnement en ligne de ne pas augmenter l'espace entre les lignes. Pour le force, il faut utiliser \displaystyle : \displaystyle\lim_{n\to\infty} donne \(\displaystyle\lim_{n\to\infty}\).
Il faudra quand même, pour la lisibilité du fichier source, veiller à laisser un espace après ces blocs. On trouvera des exemples sur cette pages qui tiendront compte de ce "gain de temps".
ATTENTION : Quitte à éviter des erreurs de frappe, je vous conseille de ne pas utiliser cette technique si vous n'êtes pas sûr du résultat. Cette technique s'acquiert petit à petit, il ne faut pas trop en demander tout de suite non plus !!
Tout document peut être divisé en plusieurs parties, chapitres, paragraphes, sous-paragraphes, etc. \(\LaTeX\), toujours aussi intelligent, possède des commandes permettant de générer directement la typographie des titres en fonction de leur importance. Il existe pour cela plusieurs commandes :
• \part{} : pour un titre de partie ;
• \chapter{} : pour un titre de chapitre (non calable dans la classe article) ;
• \section{} : pour un titre de paragraphe ;
• \subsection{} : pour un titre de sous-paragraphe ;
• \subsubsection{} : pour un titre de sous-sous-paragraphe.Les titres sont automatiquement numérotés par \(\LaTeX\) selon un format qui peut être modifié dans le préambule (en standard, les titres d'un sous-paragraphe intitulé "\(\LaTeX\)" sera par exemple "1.2.4 \(\LaTeX\)"). La commande \appendix informe \(\LaTeX\) que ce qui suit sont des annexes. Les chapitres ne porteront donc plus de numéros 1, 2 ou 3 mais la première annexe aura pour lettre A, la suivante B, etc. Ainsi, le 2ème paragraphe de la troisième annexe aura pour titre (par exemple) "C.2 Les valeurs fondamentales des mathématiques".
Vous pouvez bien évidemment expérimenter ces différences sur votre ordinateur.
Les caractères normaux s'obtiennent simplement en les tapant, y compris les accents (à condition d'avoir inclus les deux bonnes lignes dans votre préambule, voir la page Préambule si ce n'est pas le cas). Pour les formules mathématiques, les lettres grecques sont souvent indispensables. Nous les obtiendrons via les commandes \alpha, \beta, \gamma, \delta, etc. pour les lettres minuscules, et \Alpha, \Beta, \Gamma, \Delta, etc. pour les majuscules.
Les symboles mathématiques les plus utilisés sont résumés dans le tableau ci-dessous :
\infty :
\(\infty\)\star :
\(\star\)\times :
\(\times\)\% :
\(\%\)\equiv :
\(\equiv\)\neq :
\(\neq\)\geq :
\(\geq\)\n choose p :
\(n \choose p\)\leq :
\(\leq\)\subset :
\(\subset\)\not\in :
\(\not\in\)\in :
\(\in\)\forall :
\(\forall\)\ell :
\(\ell\)\exists :
\(\exists\)\Leftrightarrow :
\(\Leftrightarrow\)\Leftarrow :
\(\Leftarrow\)\Rightarrow :
\(\Rightarrow\)\cap :
\(\cap\)\stackrel{a.}{=} :
\(\stackrel{a.}{=}\)\cup :
\(\cup\)Remarques :
* Le symbole de pourcentage ne s'obtient pas en \(\LaTeX\) en tapant juste %, car \(\LaTeX\) interprète tout ce qu'il y a derrière un % comme un commentaire, et ce ne sera donc pas compilé. C'est donc l'occasion de vous dire que la commande spéciale (la seule qui ne commence pas par un \) pour faire un commentaire est %.
* Avec le package amssymb, vous pouvez obtenir de jolis symboles d'infériorité et de supériorité en remplaçant \leq et \geq par \leqslant et \geqslant : \(\leqslant\) et \(\geqslant\).En outre, puisque \(\LaTeX\) gère seul les espacements, notamment dans les formules mathématiques, il peut être judicieux de savoir comment le forcer à placer un petit espace là où vous le désirez. Il existe 5 types différents d'espace que l'on peut utiliser (\!, \,, \;, \quad et \qquad, le premier étant le seul amenant un petit retrait négatif). Regardez les exemples suivants :
\int_0^1 f(x)dx \int_0^1 f(x)\!dx \int_0^1 f(x)\,dx \int_0^1 f(x)\;dx \int_0^1 f(x)\quad dx \int_0^1 f(x)\qquad dx \(\int_0^1 f(x)dx\) \(\int_0^1 f(x)\!\!\!dx\) \(\int_0^1 f(x)\,\,dx\) \(\int_0^1 f(x)\;\,dx\) \(\int_0^1 f(x)\quad\quad dx\) \(\int_0^1 f(x)\qquad\qquad dx\) Vous pouvez bien évidemment expérimenter ces différences sur votre ordinateur.
Indice et exposants :
Dans les formules mathématiques uniquement, la mise en exposant se traduit par un "^" (ainsi m^\ell donnera \(m^\ell\)). Le même principe pour les accolades s'applique ici : si l'exposé n'est constitué que d'un seul caractère ou d'une commande (comme notre exemple ci-avant), des accolades ne sont pas nécessaires, mais dès que l'exposant est constitué de plus d'un caractère ou d'une commande, elles le deviennent. Ainsi, pour voir apparaître \(x^{a+1}\), l faudra taper x^{a+1}. La mise en indice s'effectue de manière analogue, en utilisant cette fois-ci le symbole "_" : m_\ell donnera donc \(m_\ell\).
On peut bien évidemment combiner les deux, comme le montre l'exemple suivant : n=n_1^{\alpha_1}\cdots n_p^{\alpha_p} donne \(n=n_1^{\alpha_1}\cdots n_p^{\alpha_p}\).
Notons que dans du texte, les exposants s'obtiennent via la commande \textsuperscript{exposant}. Par exemple 1\textsuperscript{er} paragraphe donnera 1er paragraphe.
Fractions, racines carrées :
La commande à utiliser pour une fraction est \frac{numérateur}{dénominateur}, ce qui donne alors : \(\frac{numerateur}{denominateur}\). Dans un calcul en ligne (expression mathématique entourée des balises $), on peut rajouter la commande \displaystyle avec \frac afin que le quotient résultant ait une taille "normale" et non réduite. Cet ajout n'est pas nécessaire lorsque l'expression mathématique est entourée des balises \[ et \] puisqu'elle y est active par défaut. Désormais, la suite de cette page fera systématiquement appel à cette commande \displaystyle pour que le résultat soit plus agréable à regarder !
Les racines carrés s'obtient en utilisant la commande \sqrt[n]{\frac1x}. [n] est optionnel : si vous le mettez, le résultat sera \(\sqrt[n]{\dfrac1x}\), alors que sans, vous verrez s'afficher \(\sqrt{\dfrac1x}\).
Les parenthèses (resp. crochets, accolades) s'obtiennent en \(\LaTeX\) en tapant () (resp. [], \{\}). Attention aux accolades : si vous mettez simplement {}, \(\LaTeX\) ne va pas considérer cela comme des accolades en soi, et on ne les verra donc pas sur le document final. Ces symboles s'ajustent à la taille de votre expression mathématique, à condition de les précéder de \left (pour ouvrir) ou de \right (pour les fermer). Ceci est très pratique pour les intervalles ou les ensembles solution :
\left[-\frac12; \frac72\right] : \left]-\infty; \frac32\right] : \scr{S} = \left\{\left(-\frac12 ; 2\right)\right\} : \scr{S} = \left{x\in\mathbb{R}|\frac1x=x\right\} : \(\left[-\dfrac12 ; \dfrac72\right]\) \(\left]-\infty ; \dfrac32\right]\) \(\scr{S} = \left\{ \left(-\dfrac12 ; 2\right) \right\}\) \(\scr{S} = \left\{ x\in\mathbb{R}\;|\;\dfrac1x=x \right\}\) Remarques :
* Nous verrons dans le paragraphe suivant comment faire les caractères incurvés et les lettres d'ensembles du dernier exemple.
* Si vous mettez un \left quelque part, il vous faudra obligatoirement un \right pour "refermer" le \left.
* Pour les systèmes d'équations, il faudra que les équations soient précédées d'une accolade ouvrante s'ajustant à la taille du système, mais pas suivie d'une accolade fermante. Dans ce cas, à la place d'écrire \right\}, nous écrirons plus simplement \right. : nous verrons un exemple dans le paragraphe 9.
En \(\LaTeX\), comme dans tout traitement de texte, il existe plusieurs polices (fontes) différentes. Les plus couramment utilisées, notamment en mathématiques sont :
\mathbb{NZDQRCH} \(\mathbb{NZDQRCH}\) \mathcal{ABCDEFGHIJKLMNOPQRSTUVWXYZ} \(\mathcal{ABCDEFGHIJKLMNOPQRSTUVWXYZ}\) \scr{ABCDEFGHIJKLMNOPQRSTUVWXYZ} \(\scr{ABCDEFGHIJKLMNOPQRSTUVWXYZ}\) Bien sûr, pour chacune des polices précédentes, on peut appliquer une graisse différente via la commande \textbf{texte mis en gras}, on peut rendre le texte italique via \textit{texte en italique}. La commande \verb"texte" permet d'afficher texte sans aucune mise en forme de la part de \(\LaTeX\). Par exemple \verb"@% cool %@ \textbf{super}" renverra @% cool %@ \textbf{super}. Nous pouvons aussi agir sur la taille de la police courante via les commandes (de la plus petite à la plus grande) \tiny, \scriptsize, \footnotesize, \small, \normalsize, \large, \Large, \LARGE, \huge et \Huge.
La police utilisée par défaut dans un document écrit en \(\LaTeX\) est "Computer Modern". Il est possible d'en changer en incluant l'un des package suivant dans le préambule : times, newcent, helvet, palatino.
Ces opérations font l'objet d'un paragraphe spécial car leur taille dépend de l'environnement dans lequel elles sont utilisées. Les exemples suivants le montrent, tout autant que la syntaxe à utiliser : dans les deux premières colonnes, il s'agit d'une utilisation "en ligne" (entre les balises $ et $) et le reste dans un environnement délimité par \[ et \].
\int_0^1 f(x) dx : \(\int_0^1 f(x) dx\) \int_0^1 \frac{f(x)}2 dx : \(\displaystyle\int_0^1 \frac{f(x)}2 dx\) \sum_{i=1}^n f(i) : \(\sum_{i=1}^n f(i)\) \sum_{i=1}^n\frac{f(i)}2 : \(\displaystyle\sum_{i=1}^n \frac{f(i)}2\) \prod_{i=1}^n f(i) : \(\prod_{i=1}^n f(i)\) \prod_{i=1}^n \frac{f(i)}2 : \(\displaystyle\prod_{i=1}^n \frac{f(i)}2\) \bigcup_{i=1}^n f(i) : \(\cup_{i=1}^n f(i)\) \bigcup_{i=1}^n \frac{f(i)}2 : \(\displaystyle\bigcup_{i=1}^n \frac{f(i)}2\) \bigcap_{i=1}^n f(i) : \(\cap_{i=1}^n f(i)\) \bigcap_{i=1}^n \frac{f(i)}2 : \(\displaystyle\bigcap_{i=1}^n \frac{f(i)}2\) \lim_{n\to\infty} u_n=2 : \(\lim {}_{n\to\infty} u_n=2\) \lim_{n\to\infty} u_n=2 : \(\displaystyle\lim_{n\to\infty} u_n=2\) Remarques :
* Notons tout de même la différence entre \cap et \bigcap : le premier sert à noter une intersection entre deux ensembles, le deuxième sert à noter une intersection entre plusieurs ensembles, généralement dépendants d'un indice.
* Tout comme \lim, il existe plusieurs fonctions prédéfinies en \(\LaTeX\) (cela veut dire qu'en les utilisant, elles n'apparaîtront pas en italique : en effet, on préfèrera \(\ln(x)\) plutôt que \(ln(x)\) : \lim, \min, \max, \ln, \exp, \cos, \sin, \tan, \arg, \lim, \inf, \sup.
Un tableau est un environnement en \(\LaTeX\) : il se code entre les balises \begin{tabular} et \end{tabular}. Ce \begin{tabular} prend un argument obligatoire que vous comprendrez mieux en regardant l'exemple ci-dessous. Dans une même ligne, un changement de case s'effectue grâce à un &, et pour changer de ligne, on utilise \\. Par exemple,
\begin{tabular}{|lc|r|} \hline
gauche & centre & droite \\ \hline
g & c & d \\
& pas de trait a gauche & mais ici oui \\ \hline
\end{tabular}\(\begin{array}{|lc|r|} \hline \text{gauche} & \text{centre} & \text{droite} \\ \hline \text{g} & \text{c} & \text{d} \\ & \text{pas de trait à gauche} & \text{mais ici oui} \\ \hline \end{array}\) Interprétation : On veut créer un document à trois colonnes. L'argument obligatoire de \begin{tabular} s'écrira donc {xxx}, où x représente la lettre l, c ou r (colonne où le texte sera respectivement aligné à gauche, au centre et à droite). La présence des traits verticaux | dans cet argument traduit qu'on souhaite une ligne avant la première colonne, entre la deuxième et la troisième, et après la dernière. Il n'y aura donc pas de ligne entre les première et deuxième colonne.
On commence donc par écrire la première ligne : gauche & centre & droite \\. Le & permet de passer d'une case à l'autre dans une ligne, et le \\ indique la fin de la ligne. Si l'on souhaite avoir un trait horizontal juste en-dessous de cette ligne (c'est-à-dire "souligner" votre texte), il suffit de rajouter \hline après le \\ (bien sûr, si l'on veut un trait horizontal tout en haut du tableau, il faut mettre le \hline juste après \begin{tabular}{|lc|r|}).Il existe deux manières différentes d'écrire des tableaux mathématiques. Soit on fait comme précédemment en mettant chaque expression d'une case entre dollars (avantage : on conserve la possibilité de faire apparaître ou non les séparations entre les lignes et colonnes ; inconvénient : beaucoup de dollars à taper, et on a souvent tendance à les oublier !!). Soit on utilise l'environnement array, qui s'utilise comme un tableau, sauf qu'on n'a pas autant de dollars à taper, mais les cases ne sont pas encadrées... À vous de voir ce qui vous arrange le mieux. Pour un tableau de variations, j'utilise par exemple un environnement tabular, dans lequel je mets effectivement chaque expression entre dollars.
Les tableaux sont particulièrement utiles pour générer des systèmes d'équations alignés. Les équations seront placées dans un tableau à trois colonnes (membre de gauche - signe "=" - membre de droite), auquel on ajoutera une accolade ouvrante devant. Attention, puisque c'est un tableau contenant des éléments mathématiques, on notera array à la place de tabular. L'exemple ci-dessous, contenant des expressions mathématiques, est à placer entre des balises $-$ ou \[-\].
\left\{ \begin{array}{rcl} x+y+z&=&1\\
y+2z&=&-2\\ z&=&0 \end{array} \right.\(\left\{ \begin{array}{rcl} x+y+z&=&1\\y+2z&=&-2\\ z&=&0 \end{array} \right.\)
Les listes sont utiles en \(\LaTeX\) pour faire une énumération de choses, ou tout simplement donner une liste non numérotées d'éléments quelconques. Voici trois exemples et les résultats qu'ils fournissent :
\begin{enumerate}
\item Premier point ;
\item Deuxième point ;
\item Troisième point.
\end{enumerate}\begin{itemize}
\item Premier point ;
\item Deuxième point ;
\item Troisième point.
\end{itemize}\begin{description}
\item["$\Leftarrow" : ] Sens indirect.
\item["$\Rightarrow" : ] Sens direct.
\end{description}

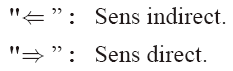
Pour la première colonne, à condition d'inclure le package enumerate dans le préambule, écrire \begin{enumerate}[(i)] à la place de \begin{enumerate} permet de remplacer automatiquement les traditionnels 1., 2. et 3. de l'exemple ci-dessus par (i), (ii) et (iii). D'autres combinaisons sont possibles, par exemple \begin{enumerate}[a)] donnera a), b) et c).
Dans la seconde colonne, cela fonctionne de manière assez analogue : pour éviter les traditionnels tirets, vous pouvez remplacer tous (histoire d'avoir le même symbole partout !) les \item par (par exemple) \item[$\diamond$] (petit losanges) ou \item[*] ou encore \item[$\bullet$] (cercle noir assez courant pour des listes).
Pour la dernière colonne, il va de soi que c'est à vous de choisir ce qu'il y aura dans les crochets, que ce soit une expression mathématique ou non...
Non mathématique :
- La commande permettant de générer automatiquement des pieds de page est \footnote{votre pied de page ici}.
- La commande \tableofcontents permet de générer une table des matières là où elle est appelée (à condition évidemment qu'il y ait des chapitres, sections, sous-sections, etc. ; et ne fonctionne que pour les classes book et report).
- \marginpar{} est une commande servant à écrire ce que vous voulez dans la marge, à l'endroit où est appelée cette commande. Pratique si votre marge est assez grande et si vous vous appelez Fermat...
- Pour écrire sur deux colonnes dans tout le document, on commencera le fichier source par (par exemple) \documentclass[twocolumn]{article}. Si vous ne voulez que deux colonnes localement (comme dans ma leçon n° 80), il vous faudra écrire votre texte dans un environnement twocolumn (c'est-à-dire qu'il faudra mettre le texte que vous voulez sur deux colonnes entre un \begin{twocolumn} et un \end{twocolumn}).
Mathématique :
- Les angles sont générés par la commande \widehat{} : \widehat{ABC} donne \(\widehat{ABC}\).
- Mes vecteurs sont obtenus par la commande \overrightarrow{AB} : \overrightarrow{} donne \(\vec{AB}\). Par contre, s'il n'y a qu'une seule lettre (minuscule) sous la flèche, préférez \vec{} (\vec{k} donne \(\vec{k}\)). Pour ne pas avoir les points sur les vecteurs i et j, utilisez \imath et \jmath.
- Le conjugué s'obtient par \bar{} : \bar{z} donne \(\bar{z}\).
- Pour mettre du texte en gras dans un environnement mathématique, placez \boldmath n'importe où dans la balise. Cette commande est très utile dans les commandes \begin{description} car tout ce qui se trouve dans les items est en gras (donc sans cette commande, le texte serait en gras, mais pas les éléments mathématiques : imaginez ce que cela donnerait sur la troisième liste ci-dessus).